规范场和杨一米尔斯方程
规范场和杨一米尔斯方程

杨一米尔斯方程(Yang-Mills equation)是一个重要的微分方程,指杨一米尔斯作用量所确定的欧拉一拉格朗日方程。杨一米尔斯方程也叫做杨—米尔斯理论。
杨氏理论是基于SU(N)组的一种量规理论,或者更普遍地说,是一个紧凑、半简单的李群。杨振宁米尔斯理论旨在描述基本粒子的行为使用这些非阿贝尔李群和统一的核心的电磁和弱力(即U(1)×SU(2))以及量子色动力学理论的强力(基于SU(3))。从而形成了我们对粒子物理标準模型理解的基础。
历史及理论
在一份私人信件中,沃尔夫冈·泡利在1953年提出了爱因斯坦的广义相对论的六维理论,将Kaluza、Klein、Fock等五维理论扩展到高维的内部空间。然而,没有证据表明泡利发展了一个量子场的拉格朗日或它的量子化。因为泡利发现他的理论“导致了一些非物质的阴影粒子”,他没有正式公布结果。虽然保利没有发表他的六维理论,但他在苏黎世发表了两份关于它的演讲。最近的研究表明,扩展的kaluza - klein理论一般不等同于杨斯-米尔斯理论,因为前者包含了额外的术语。
1954年初,杨振宁和罗伯特·米尔斯(Robert Mills)将量子电动力学(量子电动力学)的概念推广到非阿比利亚群,以解释强相互作用。杨-米尔斯的观点受到了保利的批评,因为为了保持标準的不变性,我们必须对杨-米尔斯场的量子位进行无质量控制。这一想法被搁置到1960年,当时,由Jeffrey Goldstone、Yoichiro Nambu和Giovanni jona - lasinio提出,在无质量理论中,通过对称性破环而获得质量的粒子概念被提出。
这促使了杨米尔斯理论研究的重新启动,证明了这两种理论都成功地套用了电弱统一和量子色动力学(QCD)。电弱相互作用是所描述的SU(2)×U(1)集团在量子色SU(3)杨振宁米尔斯理论。电弱理论由SU(2)与U(1)结合得到,量子电动力学(QED)由U(1)组描述,由表示弱高电荷而非电荷的U(1)组在统一电弱理论中取代。无质量的玻色子的SU(2)×U(1)理论混合后自发对称性破缺,并产生大量3弱玻色子,光子领域。统一的标準模型结合了强相互作用电弱相互作用(统一弱者和电磁相互作用)通过对称群SU(2)×U(1)×SU(3)。在目前的时代,强烈的相互作用并不是与电弱相互作用相结合,而是从耦合常数的运行中,相信它们都汇聚到一个非常高的能量的单一值。
在量子色动力学中,能量较低的现象学并没有被完全理解,因为很难用强耦合来管理这样的理论。这可能是为什幺禁闭在理论上没有被证明的原因,儘管它是一个一致的实验观察。证明了QCD在低能量範围内的限制是一个非常重要的数学问题,并由克莱数学研究所提出,无论谁也能证明杨米尔斯理论存在着一个巨大的差距及其存在。

数学定义
杨氏理论是由拉格朗日所给出的非阿贝尔对称群的一种特殊的量规理论:
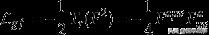
与f量(曲率或场强形式)相对应的李代数的生成器满足:

协变导数定义为:

其中,I是群生成器的标识。
该领域具有自相互作用的性质,而得到的运动方程据说是半线性的,因为非线性是同时存在且没有导数的。这意味着,只能用微扰理论来管理这一理论,有小的非线性。
我们在这里给出一些关于耦合的物理维度的注释。我们注意到,在D维度,域尺度

所以耦合必须等效于

。这意味着,对于大于4的维度,杨-米尔斯理论并没有被重新定义。此外,我们注意到,对于D = 4,耦合是无量纲的,耦合的场和方阵都有相同的场维,以及无质量的夸克标量场理论的耦合。因此,这些理论在经典层面上具有比例不变性。
量化
对于量子动力学来说,虚场解耦是因为量规组是阿贝耳曼。这可以从表栏位之间的耦合和鬼域
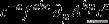
。对于阿贝尔的情况,所有的结构常数
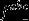
是零,所以没有耦合。在非abelian案例中,幽灵场作为一种有用的方法来重写量子场理论,而不会对诸如交叉部分或衰变率等理论的可见性产生物理影响。
杨氏理论得到的最重要结果之一是渐近自由。该结果可以通过假设耦合常数g小(小非线性),高能量和套用摄动理论得到。这一结果的相关性在于,一种描述强相互作用和渐近自由的秧子理论可以适当地处理来自深层非弹性散射的实验结果。
为了获得高能量的阳钢理论的行为,为了证明其渐近自由,一个套用摄动理论假设一个小耦合。这是在紫外线极限下验证的后验。在相反的极限情况下,红外极限,情况则相反,因为耦合太大,扰动理论难以可靠。大多数研究遇到的困难都是在低能量下管理理论。这是一种有趣的情况,是对强子物质的描述,更普遍地,对所有观察到的胶子和夸克的束缚态和它们的约束。
研究这个极限理论的最常用方法是试着在计算机上解决它。在这种情况下,需要大量的计算资源来确定无限体积(小格间距)的正确极限。这是极限,结果必须与。较小的间距和较大的耦合併不相互独立,而且每个都需要更大的计算资源。从今天开始,对于强子光谱和胶子和幽灵传播体的计算,情况似乎有些令人满意,但由于这些奇异的状态的实验观察,胶子和混合谱仍然是一个被质疑的问题。事实上,σ共振中未见任何这样的格子计算和对比提出了解释。这是一个备受争议的问题。

套用
为了理解理论在大、小动量下的行为,一个关键的量是传播器。对于一个秧苗理论,我们必须同时考虑胶子和虚传播器。在大动量(紫外线极限)下,这个问题完全解决了渐近自由的发现。在这种情况下,可以看出该理论是自由的(对于重整化群来说是微不足道的紫外固定点),而且胶子和虚传播器都是自由无质量的粒子。理论的渐近状态由带有相互作用的无质量胶子表示。
在低动量(红外极限),这个问题更需要解决。其原因是该理论在这种情况下具有很强的耦合性,不能套用摄动理论。唯一可靠的方法是在一台足够大的计算机上执行格子计算。对这个问题的回答是一个基本的问题,因为它将提供对监禁问题的理解。另一方面,我们不应该忘记,传播者是一种依赖于度量的量,因此,当一个人想要得到有意义的物理结果时,他们必须谨慎管理。
另一方面,理论方法是为了在这种情况下获得对理论的理解。先锋作品是由Vladimir Gribov和Daniel Zwanziger设计的。Gribov发现了一个关于在扬-米尔斯理论中进行测量的问题:他表明,即使一个测量值是固定的,自由也被保留了(Gribov含糊不清)。此外,他还能在朗道量表中为gluon传播者提供一种功能形式。
这种传播器不能以这种方式正确,因为它将违反因果关係。另一方面,它提供了线性上升的潜力,这将给夸克约束提供理由。这个函式形式的一个重要方面是,gluon传播器在动量为零的情况下趋于零。这将成为接下来的一个关键点。在Gribov的这些研究中,Zwanziger扩展了他的方法。不可避免的结论是,gluon的传播器应该在瞬间达到零,而在空闲的情况下,幽灵传播器应该增强。
当这个场景被提出时,计算资源不足以决定它是否正确。相反,人们採用了不同的方法,使用了镝- schwinger方程。这是一组n点函式的耦合方程,它构成了一个层次结构。这意味着n点函式的方程将依赖于(n + 1)-点函式。为了解决它们,我们需要一个适当的截断。在另一方面,这些方程是非扰动的,可以允许在任何状态下获得n点函式的行为。由Reinhard Alkofer、Andreas Hauck和Lorenz von Smekal提出了一种通过截断来解决这个层次结构的方法。
发展状况
1972年,在杰勒德·霍oft(Gerard ' t Hooft)之后,杨米尔斯理论得到了物理学界的普遍认可,他们依靠自己的导师马提尼·维尔特曼(Martinus Veltman)的一个公式来解决他们的重整化问题。(他们的工作获得了1999年诺贝尔物理学奖。)即使这个理论所描述的标準玻色子是巨大的,如在电弱理论中,只要质量只是一个“获得的”,由希格斯机制所产生的。
关于数学,应该注意到,目前,在2016年,杨-米尔斯理论是一个非常活跃的研究领域,在西蒙·唐纳森的作品中,在四维的流形上具有可微结构的不变性。此外,在陶氏数学研究所的“千年奖问题”列表中,也包括了秧歌理论。这里的奖项问题在于,尤其在一个猜想的证明中,一个纯粹的杨-米尔斯理论(即没有物质场)的最低兴奋度与真空状态有一个有限的质量差距。另一个与这个猜想有关的开放问题,是在额外的费米子粒子的存在下被限制的性质的证明。
在物理上,是从系统地套用数值方法到格点理论。



















